Удаляем стартовую страницу Webalta
4-11-2014, 18:24 Безопасность
Всем привет. Месяца 3 назад столкнулся с проблемой, связанной с Webalta. Проблема заключалась в том, что при запуске любого браузера, домашней страницей выскакивала страница поисковика Webalta. Самое интересное, что при удалении тулбара с помощью Uninstall Tool и при замене домашней станицы в браузере на нужную, ничего не менялось. При открытии браузера, домашней страницей всё равно оставалась Webalta. В этой статье я хочу рассказать как удалить домашнюю страницу webalta и о методах борьбы с этим трояном.
Вообще, Webalta это поисковик, который задумывался как альтернатива Яндексу. Разработчики обещали просто невозможное. После провала, разработчики кинули все силы на распространение поисковика через вирусы (трояны). Вирус устанавливается вместе с программой, которую вы скачали на просторах интернета.
Для начала необходимо, как сделал я, удалить тулбар программы через «установка и удаление программ». Об этом подробно рассказывать не буду, думаю, все это умеют.
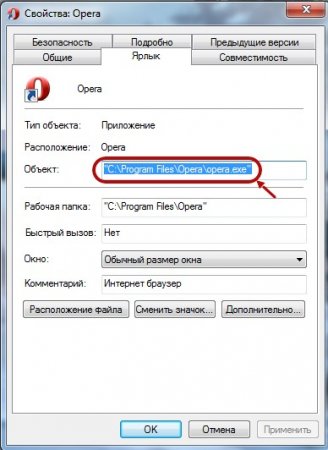
Далее изменяем домашнюю страницу в ярлыках запуска браузеров. Если вы пользуетесь одним браузером, то изменяем только в одном. Для этого жмём на ярлыке браузера правой кнопкой мыши и выбираем «Свойства». В появившемся окне удаляем всё, что идёт после «C:\Program Files\Opera\opera.exe» . Далее жмём «Применить» и "Ок”. У вас должно получиться как на картинке. Только имя браузера будет вашим.
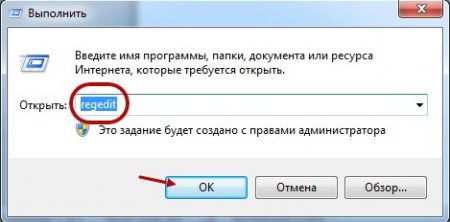
Далее чистим реестр. Для этого жмём Пуск > Стандартные > Выполнить.
В появившемся окне набираем regedit и жмём "Ок”
В новом окне нажимаем комбинацию Ctrl+F и вводим Webalta. Жмём «Найти далее»
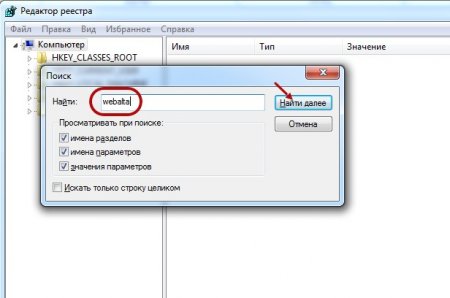
Далее удаляем все записи реестра, связанные с Webalta. Для этого жмём на записи Правой Кнопкой Мыши и в появившемся меню выбираем «Удалить». Всю процедуру проделываем несколько раз, пока в реестре не останется и следа от Webalta.
Перейдём к последнему и самому эффективному действию для удаления Webalta с вашего компьютера. Скачиваем программу Malwarebytes’ Anti-Malware . Это программа используется для нахождения и удаления троянов. Программа русскоязычная, так что проблем в использовании программы у вас не будет.
Устанавливаем и запускаем.
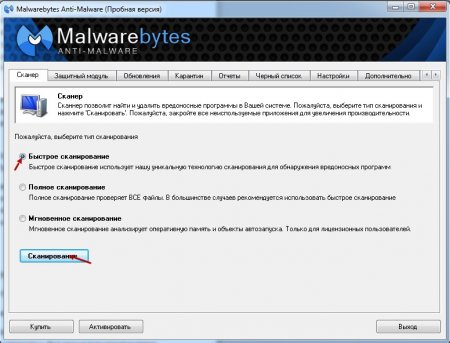
В появившемся окне выбираем «Быстрое сканирование» и жмём на кнопку «Сканировать»
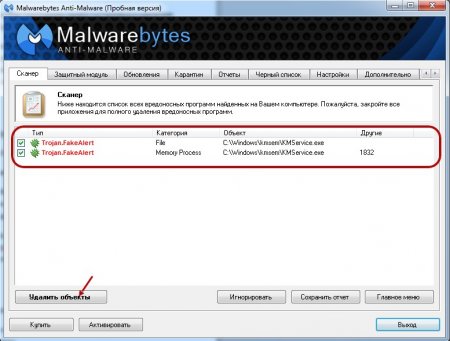
Ожидаем окончания сканирования. Далее жмём «Показать результаты» и видим примерно такую картину. В вашем случае могут быть и другие трояны.
Жмём «Удалить объекты» и после удаления перезагружаем компьютер.
На этом процесс удаления Webalta с домашней страницы вашего браузера и вашего компьютера, полностью окончен.
Далее чистим реестр.
Для этого жмём Пуск > Стандартные > Выполнить.
Кстати, комбинация Win+R — это делает мгновенно.
Надеюсь, после прочтения статьи у вас больше не возникнет вопроса «как удалить домашнюю страницу webalta?»
Помните: не устанавливайте сомнительные программы. Проблем будет больше чем пользы.
Спасибо за внимание.
Не забывайте подписываться на новости нашего блога.
Материалы по теме
 © Copyright 2024. Все права защищены.
© Copyright 2024. Все права защищены.